Research our contributions to discovery
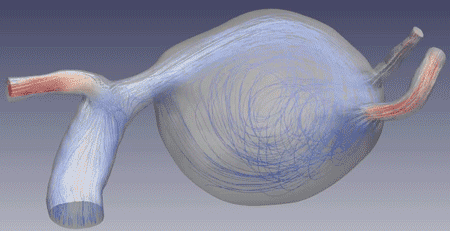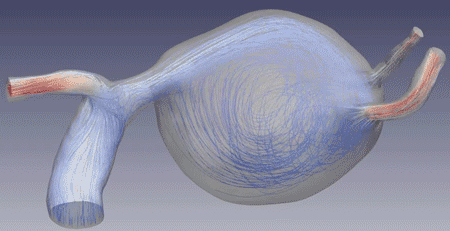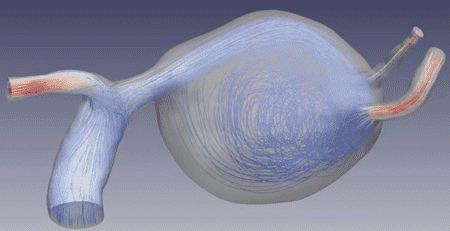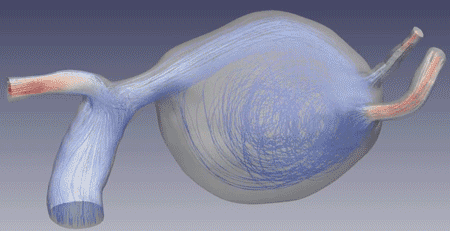
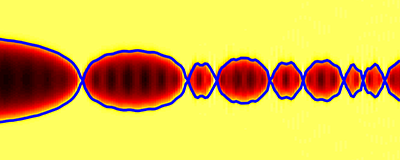
Fluid–structure interactions in cerebral aneurysms
Through a unique data set featuring patients with multiple aneurysms (with one growing and one stable, acting as "self-controls"), using patient-specific, high-resolution numerical simulations of fluid–structure interactions, we demonstrated that regions of combined low wall shear stress and oscillatory shear index correlate with aneurysmal growth. Research was supported by the Brain Aneurysm Foundation.
Micro- and nano-scale flows through deformable confinements
Flows through deformable confinements arise in microfluidics. We derived a nonlinear differential equation for a soft coating’s interface, in the presence of both fluid–structure interaction and hydrodynamic slip, to determine the conduit shape during flow. This joint research between Purdue and IIT Kharagpur was supported by the Scheme for Promotion of Academic and Research Collaboration (SPARC).
Nonlinear waves; PDEs with Hamiltonian structure; stochastics
Domain walls play a key role in condensed matter physics, cosmology, and biological physics. Their dynamics determine bulk properties of materials undergoing phase transitions, as theorized by Nobel Laureate Lev Landau. We characterized a new class of weakly localized domain walls and formulated a new theory of their interactions, overturning decades of intuition.
Nonlinear Fourier analysis and transforms for ocean acoustics modeling (NONFATFOAM)
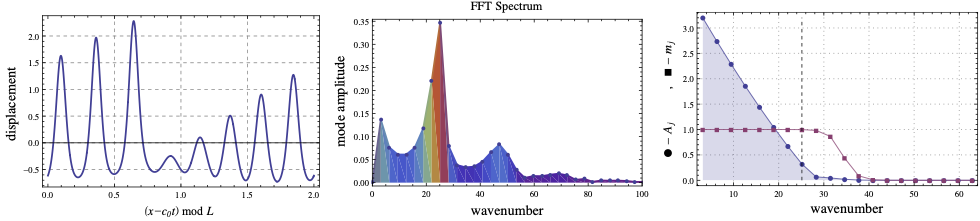
The extension of normal mode analysis to nonlinear systems is a pressing unsolved problem in engineering. The theory of nonlinear evolution equations offers an approach to generalize classical Fourier analysis on a case-by-case basis, providing a novel approach towards signal processing of nonlinear time series.
Anomalous scalings in the diffusion of granular materials
Check out our paradigm-shifting paper on the intermediate asymptotics of non-degenerate diffusion equations, contributed to the Proceedings of the National Academy of Sciences of the USA by G. I. Barenblatt himself. Research supported by the National Science Foundation.
Chaotic mixing of granular materials; 3D nonlinear dynamical systems and chaos
This was the topic of the TMNT-Lab PI's PhD dissertation. He applied advanced techniques from the theory of nonlinear dynamical systems to the problem of mixing and segregation of granular materials. Research supported by the National Science Foundation.